M203 20260124 Special functions
1. Rational Functions
1. Definition of a Rational Function
A rational function $f(x)$ as a ratio of two polynomials:
$$f(x) = \frac{P(x)}{Q(x)} = \frac{a_n x^n + a_{n-1} x^{n-1} + \dots}{b_m x^m + b_{m-1} x^{m-1} + \dots}$$
In simple terms, it's a fraction where both the numerator and denominator are algebraic expressions.
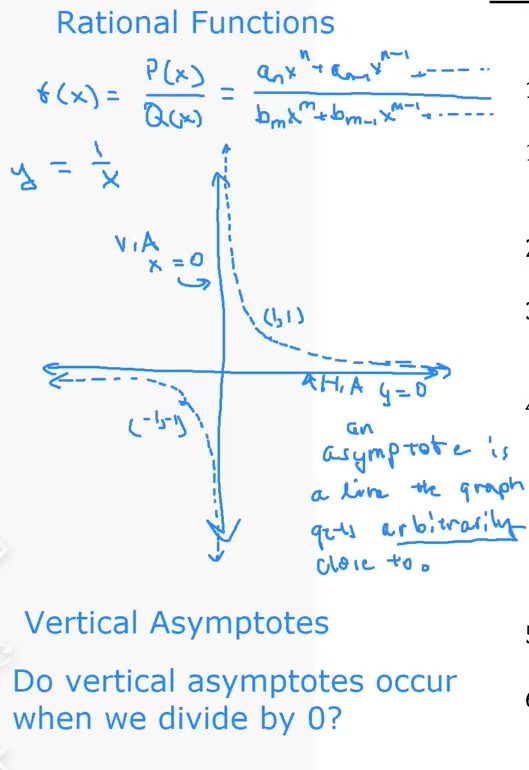
2. The Parent Function: $y = \frac{1}{x}$
The graph illustrates the most basic rational function, often called the hyperbola. It has two distinct branches in the first and third quadrants. Key points noted are $(1, 1)$ and $(-1, -1)$.
3. Asymptotes
An asymptote is a line that the graph gets "arbitrarily close to" but usually never touches.
- Vertical Asymptote (V.A.): The line $x = 0$ (the y-axis). The graph shoots up to infinity or down to negative infinity as it approaches this line.
- Horizontal Asymptote (H.A.): The line $y = 0$ (the x-axis). The graph flattens out along this line as $x$ becomes very large or very small.
4. Question: _"Do vertical asymptotes occur when we divide by 0?"_
The Answer: Essentially, yes. Vertical asymptotes occur at values of $x$ that make the denominator $Q(x) = 0$ (provided those factors don't cancel out with the numerator). Since division by zero is undefined, the function "breaks" at that point, creating a vertical boundary.
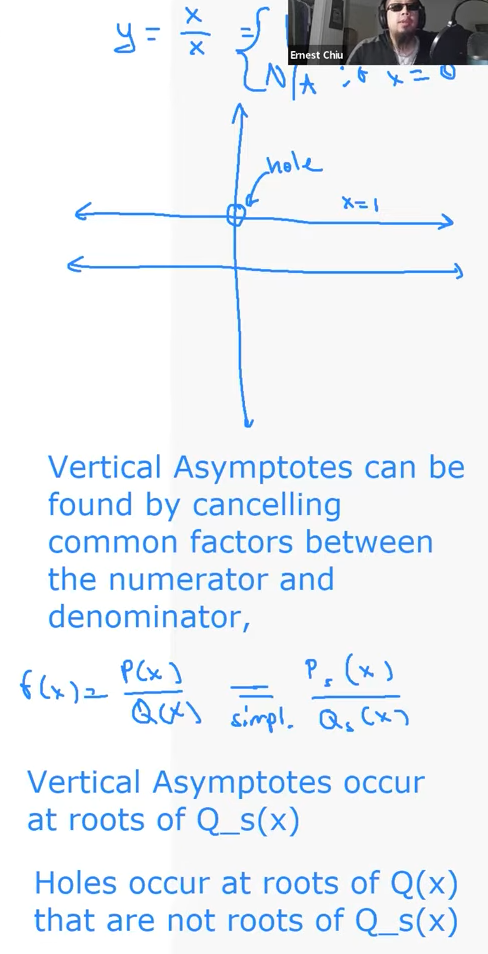
This image explains the critical distinction between Vertical Asymptotes and Holes (removable discontinuities) in rational functions.
Hidden Formula Information
Under the speaker's video feed, the function being discussed is $y = \dfrac{x}{x}$.
- The Piecewise Definition:
$$y = \frac{x}{x} = \begin{cases} 1 & \text{if } x \neq 0 \\ \text{N/A or Undefined} & \text{if } x = 0 \end{cases}$$
- The Graph: It shows a horizontal line at $y = 1$ with an open circle (hole) at the origin $(0, 1)$ because $x$ cannot be zero.
Core Concepts Explained
The image provides a step-by-step rule for identifying these features:
- Simplification: First, cancel common factors between the numerator $P(x)$ and the denominator $Q(x)$ to get the simplified version:
$$f(x) = \frac{P(x)}{Q(x)} \xrightarrow{\text{simpl.}} \frac{P_s(x)}{Q_s(x)}$$
- Vertical Asymptotes (V.A.): These occur at the roots (zeros) of the simplified denominator $Q_s(x)$. These are values that make the function blow up to infinity.
- Holes: These occur at the roots of the original denominator $Q(x)$ that were cancelled out and are no longer roots of the simplified denominator $Q_s(x)$.
Summary Table
| Feature | Where it occurs | Visual on Graph |
|---|---|---|
| Vertical Asymptote | Root of $Q_s(x)$ | A vertical dashed boundary line. |
| Hole | Root of $Q(x)$ that was cancelled | An open circle on the line/curve. |
Example:
Vertical Asymptote
1 ) $g(x)=(x^2+3x-4)/(x^2-4x+3)$, find the domain, range and all
asymptotes.
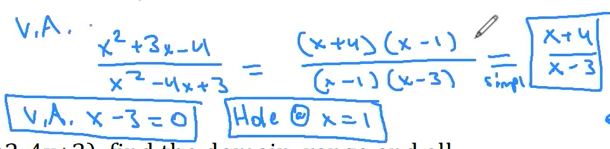
Horizontal asymptotes describe the behavior of a rational function as $x$ approaches positive or negative infinity. You can determine the horizontal asymptote ($H.A.$) of the function $f(x) = \dfrac{a_n x^n + \dots}{b_m x^m + \dots}$ by comparing the degree of the numerator ($n$) and the degree of the denominator ($m$):
Rules for Horizontal Asymptotes
- If $n < m$ (Bottom Heavy): The horizontal asymptote is always the x-axis, or $y = 0$.
- If $n = m$ (Balanced): The horizontal asymptote is the ratio of the leading coefficients: $y = \frac{a_n}{b_m}$.
- If $n > m$ (Top Heavy): There is no horizontal asymptote. (If $n = m + 1$, there is a slant/oblique asymptote instead).
Horizontal asymptote
1 ) $g(x)=(x^2+3x-4)/(x^2-4x+3)$, find the domain, range and all asymptotes.
Slope asymptote

A slant asymptote (also known as an oblique asymptote) occurs when the degree of the numerator is exactly one higher than the degree of the denominator. In the notation from your previous images, this happens when $n = m + 1$.
Instead of the graph leveling off horizontally, it follows a diagonal line as $x$ approaches infinity.
How to Find a Slant Asymptote
To find the equation of the slant asymptote, you must perform Polynomial Long Division (or synthetic division if applicable) on the rational function $f(x) = \frac{P(x)}{Q(x)}$.
1. Divide the numerator by the denominator.
2. The result will look like: $f(x) = (mx + b) + \frac{R(x)}{Q(x)}$.
3. The linear part, $y = mx + b$, is the equation of your slant asymptote.
4. As $x$ gets very large, the remainder term $\frac{R(x)}{Q(x)}$ approaches zero, which is why the graph "hugs" the line $y = mx + b$.
Example
For the function $f(x) = \dfrac{x^2 + 3x + 2}{x - 1}$:
- The degree of the numerator is 2 and the denominator is 1.
- Since $2 = 1 + 1$, a slant asymptote exists.
- After dividing, you get $f(x) = (x + 4) + \dfrac{6}{x - 1}$.
- The slant asymptote is $y = x + 4$.
Comparison of Degrees
| Condition | Type of Asymptote |
|---|---|
| $n < m$ | Horizontal ($y = 0$) |
| $n = m$ | Horizontal ($y = \frac{a_n}{b_m}$) |
| $n = m + 1$ | Slant/Oblique ($y = mx + b$) |
| $n > m + 1$ | No linear asymptote (it becomes parabolic or higher-degree) |
2 ) Let $g(x)=(2x^2-5x-1)/(x-3)$, find the asymptotes
4 ) Find the asymptotes of the following graph
• $F(x)=(x+2)/(x-1)$
• $F(x)=(x^2-1)/(2x+3)$
2. Rational Equations and Inequalities
1 ) Find all values of $x$ such that $\dfrac{x}{x-1} + \dfrac{3x-2}{x-3} = \dfrac{2-5x}{4}$
Step 1: Find the Least Common Denominator (LCD)
The denominators are $(x-1)$, $(x-3)$, and $4$. The LCD is $4(x-1)(x-3)$. Note that $x \neq 1$ and $x \neq 3$ to avoid division by zero.
Step 2: Multiply every term by the LCD to clear fractions
$$4(x-1)(x-3) \left[ \frac{x}{x-1} + \frac{3x-2}{x-3} \right] = 4(x-1)(x-3) \left[ \frac{2-5x}{4} \right]$$
Distributing the LCD gives:
$$4x(x-3) + 4(3x-2)(x-1) = (2-5x)(x-1)(x-3)$$
Step 3: Expand both sides
Left Side:
- $4x(x-3) = 4x^2 - 12x$
- $4(3x-2)(x-1) = 4(3x^2 - 3x - 2x + 2) = 4(3x^2 - 5x + 2) = 12x^2 - 20x + 8$
- Total Left Side: $(4x^2 + 12x^2) + (-12x - 20x) + 8 = 16x^2 - 32x + 8$
Right Side:
- $(x-1)(x-3) = x^2 - 4x + 3$
- $(2-5x)(x^2 - 4x + 3) = 2x^2 - 8x + 6 - 5x^3 + 20x^2 - 15x$
- Total Right Side: $-5x^3 + 22x^2 - 23x + 6$
Step 4: Set the equation to zero
Combine all terms on one side:
$$16x^2 - 32x + 8 = -5x^3 + 22x^2 - 23x + 6$$
$$5x^3 + (16x^2 - 22x^2) + (-32x + 23x) + (8 - 6) = 0$$
$$5x^3 - 6x^2 - 9x + 2 = 0$$
Step 5: Solve the cubic equation
We can test for rational roots using the Rational Root Theorem. Testing $x = 2$:
$$5(2)^3 - 6(2)^2 - 9(2) + 2 = 5(8) - 6(4) - 18 + 2 = 40 - 24 - 18 + 2 = 0$$
Since $x = 2$ is a root, $(x - 2)$ is a factor. Dividing $5x^3 - 6x^2 - 9x + 2$ by $(x - 2)$ gives:
$$(x - 2)(5x^2 + 4x - 1) = 0$$
Factoring the quadratic $5x^2 + 4x - 1$:
$$(x - 2)(5x - 1)(x + 1) = 0$$
Final Solutions
The values of $x$ are:
$$x = 2, \quad x = \frac{1}{5}, \quad x = -1$$
(All values are valid as they do not equal the restricted values of $1$ or $3$.)
Rational Inequalities
1. find domain restrictions
2. solve equality case
3. test regions
4. shade working regions
2 ) Find all real values of $x$ that satisfy $\dfrac{1}{x+1} + \dfrac{6}{x+5} \geq 1$
Inequalities often alternate between true and false regions because of the Intermediate Value Theorem. For a rational expression to change from "greater than" to "less than" a value, it must first pass through either:
1. A Zero: Where the expression equals the value.
2. A Discontinuity: Where the expression is undefined (like a vertical asymptote).
These points are called critical values. They divide the number line into intervals, and the sign of the expression generally flips when you cross one, unless that critical value comes from a squared term (like $(x-2)^2$), which would cause the graph to "touch" the axis and bounce back rather than cross it.

3. Monotonic Functions
Reasons for usefulness
1 . Min / Max are easy to find
2 . Preserve / Reflect inequalities
1 ) Find the largest possible value of $\sqrt{x+4} - \sqrt{x}$
4. Piecewise Defined Functions and Absolute Value
1) Let
$$f(x) = \begin{cases} x+5 & \text{if } x \le -3, \\ 2x^2 - 1 & \text{if } -3 < x \le 2, \\ -\frac{x}{2} & \text{if } x > 2. \end{cases} $$- Find $f(1)$, $f(9)$, $f(-12)$.
- Find $f(f(f(f(-12))))$.
- For what values of $x$ is $f(x) = x^2$?
- Graph $y = f(x)$.
2) Let
$$f(x) = \begin{cases} 2x^2 - 3, & x \le 2 \\ ax + 4, & x > 2 \end{cases}$$find $a$ if the graph is continuous.
5) If $f(x) = |2x-1|$, compute all values of $x$ for which $f(f(x)) = x$.
every absolute value equation can be solved using casework, since |x|=x or |x|=-x
IMPORTANT: we must go back and check

7 ) If $x$ and $y$ are non-zero real numbers such that $|x| + y = 3$ and $|x|y + x^3 = 0$, then what integer is closest to $x - y$?
11 ) Graph the equation $|x+1| + |y-2| = 5$
move the graph
5. Floor Function

Find all values of $x$ such that $x + \lfloor x \rfloor = 6.7$